In Chap. 15, we focused on linear mixed-effects models (LMMs), one of most widely used univariate longitudinal models in classical statistical literature and has recently been applied into microbiome data analysis. In this chapter, we introduce generalized linear mixed models (GLMMs), which can be considered as an extension of linear mixed models to allow response variables from different distributions, such as binary responses. Section 16.1 review the brief history of generalized linear models (GLMs) and generalized nonlinear models (GNLMs). Section 16.2 describes the generalized linear mixed models (GLMMs). Section 16.3 introduces model estimation in GLMMs Sect. 16.4 investigates the algorithms for parameter estimation in GLMMs and the parameter estimation algorithms for specifically developed GLMMs for microbiome research. Section 16.5 describes the statistical hypothesis testing and modeling in GLMMs.. Finally, we summarize this chapter in Sect. 16.6.
16.1 Generalized Linear Models (GLMs) and Generalized Nonlinear Models (GNLMs)
In 1972, Nelder and Wedderburn (1972) introduced a class of generalized linear models (GLMs) in univariate setting that extends the family of Gaussian-based linear model to the exponential family of distributions (i.e., assuming errors from the exponential family), in which the predicted values are determined by discrete and continuous predictor variables and by the link function (e.g., logistic regression, Poisson regression). By using the quasi-likelihood estimation approach, GLMs provide a unified approach to model either discrete or continuous data.
To account for correlated response data, Liang and Zeger in 1986 and 1988 (Liang and Zeger 1986; Zeger et al. 1988) extended the likelihood and quasi-likelihood methods to the repeated measures and longitudinal settings using a non-likelihood generalized estimating equation (GEE) via a “working” correlation matrix (Zhang et al. 2011b).
In 1988, Prentice (1988) proposed a correlated binary regression to model covariates to binary response, and in 1991, Prentice and Zhao (1991) proposed a class of quadratic exponential family that extended the exponential family to model multivariate discrete and continuous responses. These works introduced a class of generalized nonlinear models (GNLMs). In literature, the GEE approach of Liang and Zeger is a non-likelihood semiparametric estimation technique for correlated data, which is referred to GEE approach, while the approach of Prentice (1988) and Prentice and Zhao (1991) is referred to GEE2, in which the estimation and inference are based on the second-order generalized equations.
GLMs and GNLMs share one common characteristic: their inferences are based the parameters that model an underlying marginal distribution. In other words, both GLMs and GNLMs are used to estimate the regression parameters that predict the average response in a population of individuals and model the effects of different covariates on the mean response of a given population (Vonesh 2012) (p. 205).
16.2 Generalized Linear Mixed Models (GLMMs)
In contrast to the population-averaged inference of GLMs and GNLMs, GLMMs focus on the subject-specific inference, in which the regression parameters estimate the “typical” or “average” individual’s mean response instead of the average response for a population of individuals (Vonesh 2012). GLMMs combine statistical frameworks of linear mixed models (LMMs) and generalized linear models (GLMs): extending the properties of (1) LMMs via incorporating random effects and (2) GLMs by using link functions and exponential family distributions to allow response variables to handle non-normal data (e.g., Poisson or binomial). By combining the statistical frameworks of both LMMs and GLMs, GLMMs extend the capability of GLMs for handling non-normal data (e.g., logistic regression) (McCullagh and Nelder 2019) by using both fixed and random effects in the linear predictor (hence become mixed models) (Breslow and Clayton 1993; Stroup 2012; Jiang and Nguyen 2021).
The extension of the GLM of Nelder and Wedderburn (1972) to GLMMs through a number of publications in the mid-1980s and early 1990s such as mostly by Stiratelli et al. (1984), Zeger et al. (1988), Schall (1991), and Breslow and Clayton (1993). All the models proposed in these papers are limited to the conditionally independent models, i.e., they all considered that observations within clusters or subjects are conditionally independent given a set of random effects (Vonesh 2012). In 1993, Wolfinger and O’Connell (1993) extended the basic formulation by also allowing for within-cluster or within-subject correlation, and then a general equation of GLMMs is formulated (Vonesh 2012).
Assume yi is a vector of grouped/clustered outcome for the ith sample unit (i = 1, …, n), and then GLMMs are generally defined as:
![$$ g\left[E\left({y}_i|{b}_i\right)\right]={X}_i\beta +{Z}_i{b}_i, $$](images/486056_1_En_16_Chapter_TeX_Equ1.png)
Because the fixed effects (including the intercept of fixed effect) are directly estimated, what is left to estimate is the variance. In other words, the random effect complements are to model the deviations from the fixed effect, and the random effects are just deviations around the mean value in β and hence have mean zero. For a random intercept, the variance of the random intercept is just a 1 × 1 matrix. If a random intercept and a random slope are specified, then random effect complement is a variance-covariance matrix. This matrix has some properties such as square, symmetric, and positive semidefinite as well as redundant elements. For a q × q matrix, there are q(q + 1)/2 unique elements. Typically this matrix is estimated via θ (e.g., a triangular Cholesky factorization G = LDLT) rather than is directly modeled.
In order to remove the redundant effects to simplify computation and ensure that the resulting estimate matrix is positive definite, usually, we can use various different ways to parameterize G and use various constraints to simplify the model. For example, we can (1) consider G representing the random effects and use the nonredundant elements such as taking the natural logarithm to ensure that the variances are positive and (2) assume the random effects have the simplest independent structure. Thus, the final element in the model is the variance-covariance matrix of the residuals, ε or the conditional covariance matrix of yi ∣ Xiβ + zibi.
If we assume a homogeneous residual variance for all (conditional) observations and that they are (conditionally) independent, then the most common residual covariance structure is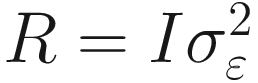 
, where I is the identity matrix (diagonal matrix of 1s) and 
is the residual variance. We can also assume other structures such as compound symmetry or autoregressive.
In the terminology of SAS, the variance-covariance matrix of the random effects is G matrix, while the residual covariance matrix of the random effects is R matrix. Thus, in GLMMs the final fixed elements are yi, Xi, zi, and ε. The final estimated elements are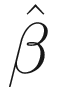 
, 
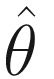, and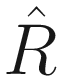 
. The final model depends on the assumed distribution but generally has the form:
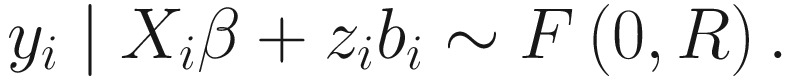
In addition, the distribution may potentially have extra dispersion/shape parameters.
16.3 Model Estimation in GLMMs
GLMMs are relatively easy to perform. To fit the data, basically it is to just specify a distribution, link function, and structure of the random effects. Because the differences between groups can be modeled as a random effect, GLMMs provide a various models to fit the grouped data, including longitudinal data (Fitzmaurice et al. 2012).
GLMMs are fitted via maximum likelihood (ML), which involves integrating over the random effects. In general because the random effects in GLMMs are nonlinear, the marginal log-likelihood function or the marginal moments of GLMMs do not have closed form of expressions except in special cases (e.g., in linear mixed-effects model). In particular, the log-likelihood function of the observed yi is given:
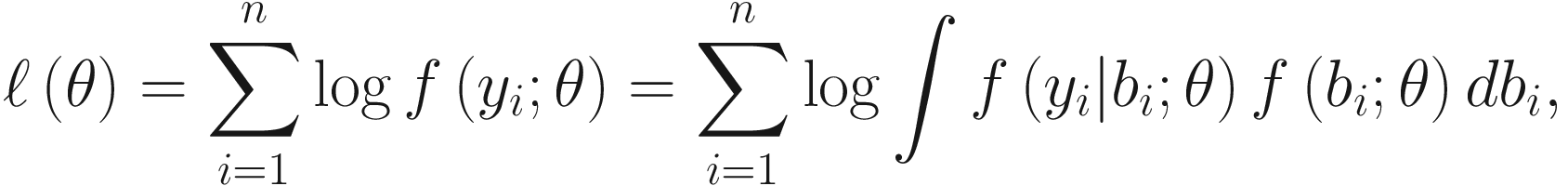
ML estimation requires maximization of the integral in (16.1), which in special cases (e.g., in linear mixed-effects model) can be evaluated analytically and maximized by standard methods (Raudenbush et al. 2000) such as the EM (Dempster et al. 1977, 1981), Fisher scoring (Goldstein 1986; Longford 1987), or Newton-Raphson (Lindstrom and Bates 1988). However, although the integrals and hence the log-likelihood function ℓ(θ) seem simple in appearance and generally do not have a resolution of closed analytical form because to obtain the ML estimates, it needs to integrate likelihoods over all possible values of the random effects (Browne and Draper 2006; Lele 2006), i.e., a potentially high dimensional integration is needed when a large number of random effects (i.e., high dimension of bi) is specified (Zhang et al. 2011a). Thus, the ML estimation usually requires numerical approximations.
16.4 Algorithms for Parameter Estimation in GLMMs
Various estimators have been proposed. The advantages and disadvantages of these algorithms and the software packages that implement these methods have been compared by the review articles such as Pinheiro and Chao (2006) and Bolker et al. (2009), as well as simulation studies such as Raudenbush et al. (2000), Zhang et al. (2011a), and Zhang and Yi (2020).
Zhang et al. (2011a) divided the estimation into (1) approximating the model using linearization and (2) approximating the log-likelihood function.
Vonesh (2012) divided the estimation for generalized linear and nonlinear models into (1) a moment-based approach utilizing some form of Taylor-series linearization and (2) a likelihood-based approach using some form of numerical integration.
Actually the approach of approximating the model and the moment-based approach stated a similar thing: using Taylor-series expansion to approximate the marginal moments (first- and second-order conditional moments) and hence approximate the model.
Raudenbush et al. (2000) grouped the estimation as three prominent strategies: (1) quasi-likelihood inference; (2) Gauss-Hermite approximations; and (3) Monte Carlo integration.
In this chapter, we categorize four algorithms for estimation in GLMMs: (1) penalized quasi-likelihood-based methods using Taylor-series linearization; (2) likelihood-based methods using numerical integration; (3) Markov Chain Monte Carlo-based integration; and (4) IWLS (Iterative Weighted Least Squares) and EM-IWLS algorithms.
Among the various estimation techniques that have been proposed for estimating the parameters of GLMMs, linearization via Taylor series expansion and numerical integration are the most frequently used techniques. Taylor series linearization techniques are used to approximate either the marginal moments of an approximate marginal quasi-likelihood function (Zhang et al. 2011a; Vonesh 2012) or an integrated quasi-likelihood function corresponding to specified first-and second-order conditional moments (Vonesh 2012). Numerical integration techniques are used exclusively for estimation based on maximizing an integrated log-likelihood function. Particularly, the methods involving numerical quadrature (e.g., via Gauss-Hermite quadrature) or Markov chain Monte Carlo and Laplace approximation (Breslow and Clayton 1993) have increased in use due to increasing computing power and advances in methods in practice. Recently in microbiome field, IWLS algorithm and its extension of EM-IWLS algorithm have been increased in use.
16.4.1 Penalized Quasi-Likelihood-Based Methods Using Taylor-Series Linearization
This category can combine the approaches of pseudo-likelihood (PL) (Wolfinger and O’Connell 1993) and penalized quasi-likelihood (PQL) (Breslow and Clayton 1993). The PQL approach was termed by Breslow and Clayton (1993). Because the GLMM is nonlinear in the random effects, this approach approximates to the first- and second-order conditional moments of the model (Vonesh 2012) using linearization. Typically a doubly iteration algorithm is involved in linearization (Zhang et al. 2011a): First, the GLMM is approximated by a linear mixed-effects model based on current values of the covariance parameter estimates, and then the resulting linear mixed-effects model is fitted iteratively, and once convergence the linearization is updated using the new parameter estimates, resulting in a new linear mixed-effects model. The iterative process continues until the difference in parameter estimates between successive linear mixed model fits fall within a specified tolerance level.
Can fit models with a large number of random effects, crossed random effects, multiple types of subjects, and even correlated response after conditioning on covariates in fixed effects and zero-inflated terms and random effects (Zhang et al. 2011a). Thus the PQL approach is flexible and widely implemented (Bolker et al. 2009).
The linearized model has a relatively simple form that typically can be fitted based only on the mean and variance in the linearized form (Zhang et al. 2011a).
PQL computes a quasi-likelihood rather than a true likelihood. It is inappropriate to use quasi-likelihoods to make likelihood-based inference (Bolker et al. 2009; Pinheiro and Chao 2006). Thus, PQL algorithm only generates Wald-type test statistics and cannot perform likelihood-based tests such as the likelihood ratio statistic (Zhang et al. 2011a).
PQL is inconsistent and is biased for estimates of regression coefficients. The bias is severely for sparse within-subject data (Breslow and Lin 1995; Lin and Breslow 1996), is very severe particularly for paired binary data (Breslow and Lin 1995; Breslow and Clayton 1993), and is most serious when the random effects have large variance and the binomial denominator is small (Raudenbush et al. 2000). Thus, although it was shown that the PQL estimator is consistent upon its order in terms of effect of cluster size, and even for discrete binary data (Vonesh et al. 2002) and is closely related to the Laplace-based ML estimator in some conditions (Vonesh 2012), in general, PQL estimator is biased for large variance or small means (Bolker et al. 2009).
Particularly PQL estimator has poor performance for Poisson data when the mean number of counts per treatment is less than five, or for binomial (also binary) data if the expected numbers of successes and failures for each observation are both less than five (Breslow 2003).
Even the algorithms that implement linearization can fail at both levels of the double iteration scheme (Zhang et al. 2011a).
16.4.2 Likelihood-Based Methods Using Numerical Integration
In contrast to the PQL approach using linearization, numerical integration approach solves the nonlinear issue of the random effects usually by approximating the marginal log likelihood (Vonesh 2012), which can be achieved via a singly iterative algorithm. Laplace approximation (Raudenbush et al. 2000; Breslow and Lin 1995; Lin and Breslow 1996), Gauss-Hermite quadrature (GHQ) (Pinheiro and Chao 2006; Anderson and Aitkin 1985; Hedeker and Gibbons 1994, 1996), and Adaptive Gauss-Hermite quadrature (AGQ) (Pinheiro and Bates 1995) can be categorized into this approach. We introduce them separately.
16.4.2.1 Laplace Approximation
Laplace approximation has a long history that used for approximating integrals and is often used in a Bayesian framework for approximating posterior moments, marginal densities (Vonesh 2012; Tierney and Kadane 1986). It is a special case of the GHQ with only one quadrature point (Bates et al. 2015).
Approximates the true GLMM likelihood rather than a quasi-likelihood (Raudenbush et al. 2000).
Is more accurate than PQL (Bolker et al. 2009). Particularly it was shown that sixth-order Laplace approximation was much faster than those required non-adaptive GHQ and AGQ, and produced comparable good results by the Gauss-Hermite method with 20 quadrature points and adaptive method with seven quadrature (Raudenbush et al. 2000).
Like PQL estimator, Laplace-based ML estimator is consistent upon its order in terms of effect of cluster size and even for discrete binary data (Vonesh 1996).
Produces estimates with unknown asymptotic properties due to not maximizing the underlying log-likelihood function, and hence it may not provide reliable and consistent estimates, except in the special linear mixed-effects model the maximum likelihood estimation (MLE) is really produced by this approach (Lindstrom and Bates 1988).
Like PL and PQL, Laplace-based ML estimator is biased for estimates of regression coefficients. The bias is severe for sparse within-subject data (Breslow and Lin 1995; Lin and Breslow 1996) and is very severe particularly for paired binary data (Breslow and Lin 1995; Breslow and Clayton 1993).
Is slower and less flexible than PQL.
16.4.2.2 Gauss-Hermite Quadrature (GHQ)
Is more accurate (Pinheiro and Chao 2006; Bolker et al. 2009) because GHQ yields estimates that approximate the MLE (Zhang et al. 2011a).
GHQ overcomes the small sample bias associated with Laplace approximation and PQL (Pinheiro and Chao 2006), and thus GHQ is recommended for highly discrete data. In contrast, we should not use Laplace approximation and PQL unless the cluster sizes are larger or the random-effects dispersion is small (Vonesh 2012).
16.4.2.3 Adaptive Gauss-Hermite Quadrature (AGQ)
Is much more difficult as the number of correlated random effects per cluster increases (Raudenbush et al. 2000).
It was shown that the R packages lme4 and glmmML using the integral approach based on AGQ do not seem to provide more accurate estimates than its Laplace counterpart for these packages as in its SAS NLMIXED when fitting binary responses (Zhang et al. 2011a).
Mean squared errors of AGQ with seven quadrature are larger than those of sixth-order Laplace approximation and the average run time for the AGQ analyses was very slower compared to sixth-order Laplace approximation (Raudenbush et al. 2000).
16.4.3 Markov Chain Monte Carlo-Based Integration
Markov chain Monte Carlo(MCMC) integration methods (Wei and Tanner 1990) generate random samples from the distributions of parameter values for fixed and random effects rather than explicitly integrate over random effects to compute the likelihood (Bolker et al. 2009). MCMC is usually used in a Bayesian framework (McCarthy 2007); it either incorporates prior information from previous knowledge about the parameters or specifies uninformative (weak) prior distributions to indicate without knowledge (McCarthy 2007). Thus in MCMC inference is based on summary statistics (i.e., mean, mode, quantiles, etc.) of the posterior distribution, which combines the prior distribution with the likelihood (McCarthy 2007).
Is highly flexible, arbitrary number of random effects can be specified (Bolker et al. 2009; Gilks et al. 1995).
Bayesian MCMC is similarly accurate to maximum-likelihood approaches when datasets are highly informative and little prior knowledge is assumed. There are two reasons that MCMC does not need assumption (Bolker et al. 2009): First, MCMC provides confidence intervals on GLMM parameters by naturally averaging over the uncertainty in both the fixed and random-effect parameters and hence avoiding most difficult approximations used in frequentist hypothesis testing. Second, Bayesian techniques define posterior model probabilities that automatically penalize more complex models, hence providing a way to select or average over models.
It is very slow, involving potentially technically challenging (Bolker et al. 2009), such as requiring the statistical model is well posed, choosing appropriate priors (Berger 2006), and efficient algorithms for large problems (Carlin 2006), and assessing when chains have run long enough for reliable estimation (Cowles and Carlin 1996; Brooks and Gelman 1998; Paap 2002).
It is computationally intensive and is convergent stochastically rather than numerically, which can be difficult to assess (Raudenbush et al. 2000).
Some users do not favor the Bayesian framework (Bolker et al. 2009).
16.4.4 IWLS and EM-IWLS Algorithms
IWLS (iterative weighted least squares) algorithm is used to find the maximum likelihood estimates of a generalized linear model (Nelder and Wedderburn 1972; McCullagh and Nelder 1989). The standard IWLS algorithm is equivalent to PQL procedure. In 2017, Zhang et al. (2017) extended the commonly used IWLS algorithms for fitting generalized linear models (GLMs) and generalized linear mixed models (GLMMs) for fitting negative binomial mixed models (NBMMs) to analyze microbiome data with the independent within-subject errors in the linear mixed model.
In 2018, the same research group (Zhang et al. 2018) applied the IWLS algorithms to fit the NBMMs for longitudinal microbiome data to account for special within-subject correlation structures. In 2020, they (Zhang and Yi 2020) applied the IWLS algorithms again to fit zero-inflated negative binomial mixed models (ZINBMMs) for modeling longitudinal microbiome data to account for excess zeros in the logit part.
16.4.4.1 Extension of IWLS Algorithm for Fitting NBMMs
The extended IWLS algorithm for fitting NBMMs (Zhang et al. 2017) was developed based on the standard IWLS (equivalently PQL). Basically, the extension of the IWLS algorithm to NBMMs is used to iteratively approximate the negative binomial mixed model by a linear mixed model via iteratively updating the parameters of the fixed and random effects, within-subject correlation and fixed shape. Like quasi-GLMs (McCullagh and Nelder 1989) and GLMMs (Venables and Ripley 2002; Schall 1991; Breslow and Clayton 1993), the extended IWLS algorithm for fitting the NBMMs introduces a dispersion parameter to correct for over-dispersion to some extent even if shape parameter is not well estimated.
- 1.
Updating the parameters of the fixed and random effects, within-subject correlation by extending the IWLS algorithm (or equivalently the PQL procedure) for fitting GLMMs (Breslow and Clayton 1993; Schall 1991; Searle and McCulloch 2001; Venables and Ripley 2002; McCulloch and Searle 2004). The IWLS algorithm first uses a weighted normal likelihood to approximate the generalized linear model likelihood and then updates the parameters from the weighted normal model (McCullagh and Nelder 1989; Gelman et al. 2013), i.e., in the NBMMs case, the negative binomial (NB) likelihood can be approximated by the weighted normal likelihood conditional on the shape parameter, the fixed, and the random effects (Zhang et al. 2017).
- 2.
Updating the shape parameter by maximizing the NB likelihood using the standard Newton-Raphson algorithm conditional on the fixed and random effects (Venables and Ripley 2002).
Using the standard procedure for fitting the linear mixed models (Zhang et al. 2017) because it was developed based on the commonly used algorithms for fitting GLMs and GLMMs.
Flexibility, stability and efficiency (Zhang et al. 2017).
Being robust and efficient to deal with over-dispersed microbiome count data (Zhang et al. 2017) because it overcomes the issues (Saha and Paul 2005) of the lack of robustness, being severely biased and especially failure to converge for small sample size with the ML estimator of the shape parameter in NB models by adding a dispersion parameter to the framework of GLMMs,
16.4.4.2 Extension of IWLS Algorithm for Fitting Longitudinal NBMMs
Not only can address over-dispersion and varied total reads in microbiome count data but also account for correlation among the observations (non-constant variances or special within-subject correlation structures) (Zhang et al. 2018).
Is stable and efficient (Zhang et al. 2017, 2018) and flexible to handle complex structured longitudinal data, allowing for incorporating any types of random effects and within-subject correlation structures as in Pinheiro and Bates (2000) and McCulloch and Searle (2001).
16.4.4.3 EM-IWLS Algorithm for Fitting Longitudinal ZINBMMs
The EM-IWLS algorithm for fitting longitudinal ZINBMMs (Zhang and Yi 2020) was developed (1) to distinguish the logit part for excess zeros and the NB distribution via a latent indicator variable; (2) to iteratively approximate the logistic likelihood using a weighted logistic mixed model via the standard IWLS algorithm (equivalently PQL procedure) for fitting GLMMs (Breslow and Clayton 1993; Schall 1991; Searle and McCulloch 2001; Venables and Ripley 2002); and (3) to update the parameters in the means of the NB part via the extended IWLS algorithm (Zhang et al. 2017).
Is able to model over-dispersed and zero-inflated longitudinal microbiome count data (Zhang and Yi 2020).
Like other ZINBMM methods (Zhang et al. 2017, 2018), FZINBMM method takes advantage of the standard procedure of fitting LMMs to facilitate handling various types of fixed and random effects and within subject correlation structures (Zhang and Yi 2020).
Particularly, it was demonstrated that the EM-IWLS algorithm has remarkable computational efficiency and statistically comparable with the adaptive Gaussian quadrature algorithm in GLMMadaptive package and the Laplace approximation in the glmmTMB package in terms of empirical power and false positive rates (Zhang and Yi 2020). Both GLMMadaptive and glmmTMB packages use numerical integration to fit ZINBMMs.
Thus, FZINBMM method is fast and stable because of using model-fitting EM-IWLS algorithm.
Various algorithms for parameter estimation have been evaluated based on speed and accuracy. As the techniques advance, nowadays computer is running much fast, the difference of running time for different algorithms is within minutes, thus accuracy is much more important than speed.
16.5 Statistical Hypothesis Testing and Modeling in GLMMs
In this section, we review and describe some problems for performing statistical hypothesis testing and modeling in GLMMs including GLMs and ZIGLMM.
16.5.1 Model Selection in Statistics
Model selection is a crucial step in big data science including microbiome data analysis for reliable and reproducible statistical inference or prediction. The goal of model selection is to select an optimal statistical model from a set of candidate models based on a given dataset.
In statistics, model selection is defined from the perspective of “procedure,” in which model selection can be defined as a pluralism of different inferential paradigms by using either statistical null hypothesis testing approach (Stephens et al. 2005) or the information-theoretic approach (Burnham and Anderson 2002). The null hypothesis testing method is to test the simpler nested models against more complex models (Stephens et al. 2005), while the information-theoretic method attempts to identify the (likely) best model, orders the models from the best to worst, and weights the evidence of each model to see if it really is the best as an inference (Burnham and Anderson 2002) (p. ix).
These two approaches may result in substantially different models being selected. Although the information-theoretic approach has been considered to offer powerful and compelling advantages over null hypothesis testing, the null hypothesis testing approach has their own benefits (Stephens et al. 2005). Both approaches actually have their own strengths and weaknesses depending on what kinds of data are used for the model selection.
16.5.2 Model Selection in Machine Learning
In machine learning, model selection is defined from the perspective of “objective,” in which model selection can be defined as two directions and two roles they play, respectively: model selection for inference and model selection for prediction (Ding et al. 2018b). The goal of the first direction is to identify the best model for the data, thus for scientific interpretation the selected model is required not too sensitive to the sample size, which accordingly requires the evaluating methods can select the candidate model most robustly and consistently (Ding et al. 2018b). The goal of the second direction is to choose a model as machinery to offer excellent predictive performance. Thus, the selected model may simply be the lucky winner among a few close competitors, but the selected model should have the predictive performance as best as possible (Ding et al. 2018b).
When model selection is defined in two directions, it emphasizes the distinction of statistical inference and prediction. For example, Ding et al. (2018b) thought that (1) better fitting does not imply better predictive performance and (2) the predictive performance is optimal at a candidate model that typically depends on both the sample size and the unknown data-generating process. Thus, practically an appropriate model selection technique in parametric framework should be able to strongly select the best model for inference and prediction, while in nonparametric framework, it should be able to strike a good balance between the goodness of fit and model complexity on the observed data to facilitate optimal prediction.
Model selection defined from statistics and machine learning share a common objective: statistical inference. Whether model selection is defined based on the “procedure” or the “objective,” the key is to select the (likely) best model. We summarize the important criteria of model selection used in the literature and put our thoughts on model selection in general and model selection specifically for microbiome data.
16.5.3 Information Criteria for Model Selection
Here we introduce some information criteria for model selection in GLMMs, including GLMs and ZIGLMMs whose asymptotic performances are well understood. Generally Information Criteria refer to model selection methods for parametric models using likelihood functions. A number of model selection criteria have been developed and investigated based on estimating Kullback’s directed or symmetric divergence (information theory and statistics) (1968) (Kullback 1997). In general, information criteria is to quantify the Kullback-Leibler distance to measure the relative amount of information lost when a given model approximates the true data-generating process (Harrison et al. 2018).
16.5.3.1 AIC (Akaike’s Information Criterion)
AIC (Akaike 1973, 1974; Burnham and Anderson 2004; Aho et al. 2014) was proposed to justify for a large-sample estimator of Kullback’s directed divergence between the generating model and a fitted candidate model (Kim et al. 2014). AIC was developed based on the asymptotic properties of ML estimators and hence was considered by Akaike as an extension of R. A. Fisher’s likelihood theory (Burnham and Anderson 2002) (p. 3). AIC is defined as:
AIC can be used for comparing non-nested models.
The smaller the AIC value, the better the model. Thus, the model with the lowest AIC indicates the least information lost and hence represents the best model in that it optimizes the trade-off between fit and complexity (Richards 2008).
This statistic takes into consideration model parsimony penalizing for the number of predictors in the model. Thus, more complex models (with larger k) will suffer from larger penalties.
AIC (a minimax optimal criterion) is safer for use than BIC when model selection is for prediction because the minimax consideration gives more protection in the worst case (Ding et al. 2018b).
When the number of case (the sample size) N is small and k is relatively large (e.g., k ≃ N/2), AIC severely underestimates Kullback’s directed divergence and results in inappropriately favoring unnecessarily large (or high dimensional candidate) models (Hurvich and Tsai 1989; Kim et al. 2014).
Specifically for GLMMs, the use of AIC has two main concerns (Bolker et al. 2009): one is the boundary effects (Greven 2008) and another is the estimation of degrees of freedom for random effects (Vaida and Blanchard 2005).
16.5.3.2 AICc (Finite-Sample Corrected AIC)
AICc was originally proposed by Sugiura (1978) in the framework of linear regression models with normal errors. Then it was extended into various frameworks (e.g., normal and nonlinear regression) (Hurvich and Tsai 1989; Hurvich et al. 1990), which was proposed as an improved estimator of Kullback-Leibler information to correct the AIC for small samples. AICc is defined as:
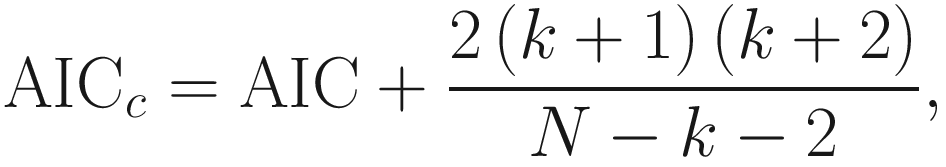
It selects the model that minimizes AICc.
There is little difference between AICc and AIC unless the number of case N is small compared with model dimension.
It is less generally applicable compared to AIC because the justification of AICc is depending on the structure of the candidate modeling framework.
16.5.3.3 QAIC and QAICc (Quasi Akaike Information Criterion and Corrected Quasi-AIC)
For over-dispersed count data, the simple modified versions of AIC and AICc have been increasingly utilized (Burnham and Anderson 2002; Kim et al. 2014). Specifically, the quasi Akaike information criterion (quasi-AIC, QAIC) and its corrected version, QAICc (Lebreton et al. 1992), have been proposed as the quasi-likelihood analogues of AIC and AICc for modeling over-dispersed count or binary data. They are defined as below:
![$$ \mathrm{QAIC}=-\left[\frac{2\log (L)}{\hat{c}}\right]+2k, $$](images/486056_1_En_16_Chapter_TeX_Equ6.png)
![$$ {\displaystyle \begin{array}{c}{\mathrm{QAIC}}_c=-\left[\frac{2\log (L)}{\hat{c}}\right]+2k+\frac{2k\left(k+1\right)}{N-k-1}\\ {}=\mathrm{QAIC}+\frac{2k\left(k+1\right)}{N-k-1},\end{array}} $$](images/486056_1_En_16_Chapter_TeX_Equ7.png)
Here, c is a single variance inflation factor used for approximation in modeling of count data (Cox and Snell 1989). The formulas for QAIC and QAICc will reduce to AIC and AICc, respectively, when no over-dispersion exists (i.e., c = 1). The variance inflation factor c should be estimated from the global model, i.e., the candidate model that contains all covariates of interest and hence subsuming all of the models in the candidate family (Burnham and Anderson 2002; Kim et al. 2014). In practice, it can be estimated from the goodness-of-fit chi-square statistic (χ2) of the global model and its degrees of freedom,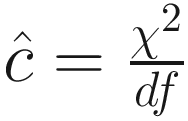 
.
The reason that QAIC and QAICc were developed because when count data are over-dispersed and c > 1, the proper likelihood is log(L)/c instead of just log(L), i.e., the quasi-likelihood methods are appropriate. Researchers have found that QAIC and QAICc performed well for analyzing different levels of over-dispersion in product multinomial models (Anderson et al. 1994) because the quasi-likelihood criteria tend to outperform the ordinary likelihood criteria when dealing with over-dispersed count data (Kim et al. 2014). Because “quasi-likelihood methods of variance inflation are most appropriate only after a reasonable structural adequacy of the model has been achieved” (Burnham and Anderson 2002) in characterizing the mean, thus c should be computed only for the global model. However, we should note that although the estimation of c based on the global model is recommended, some standard software packages (e.g., SAS GENMOD) do not estimate the single variance inflation factor c using the global model (Burnham and Anderson 2002).
16.5.3.4 BIC (Bayesian Information Criterion)
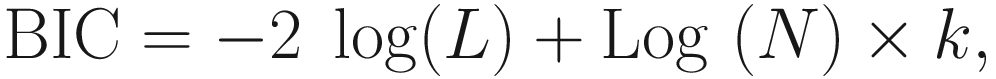
Like AIC, the smaller the BIC value, the better the model.
Also like AIC, the penalties are there to reduce the effects of overfitting.
The penalty is stronger for BIC than AIC for any reasonable sample size.
BIC often yields oversimplified models because BIC imposes a harsher penalty for the estimation of each additional covariate.
BIC performs better than AIC when the data have large heterogeneity due to the stronger penalty (Brewer et al. 2016).
As a variant of AIC, BIC is useful when one wants to identify the number of parameters in a “true” model (Burnham and Anderson 2002).
Both BIC and AICc perform penalty based on total sample size; compared to AICc, BIC penalize more severe for moderate sample sizes and penalize less severe for very low sample size (Brewer et al. 2016).
16.5.3.5 BC (Bridge Criterion)
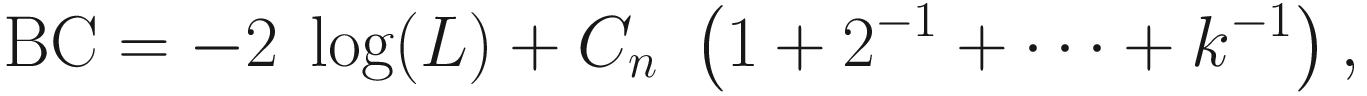
BC aims to bridge the advantages of both AIC and BIC in the asymptotic regime (Ding et al. 2018a).
The penalty is approximately Cn log (k), but it is written as a harmonic number for its nice interpretation (Ding et al. 2018b).
BC performs similarly to AIC in a nonparametric framework and similarly to BIC in a parametric framework (Ding et al. 2018a, b).
BC was shown achieving both consistency when the model class is well-specified and asymptotic efficiency when the model class is mis-specified under mild conditions (Ding et al. 2018a).
16.5.3.6 DIC (Deviance Information Criterion)
DIC (Spiegelhalter et al. 2002) is defined as:
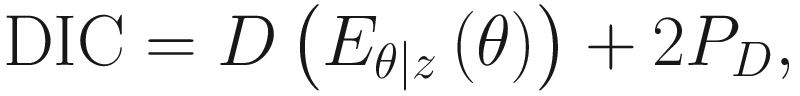
DIC selects the model that minimizes the equation. DIC is defined with a relevant concept, the deviance under model: D(θ) = − 2 log P(y| θ) + C and the effective number of parameters of the model: PD = Eθ ∣ zD(θ) − D(Eθ ∣ z(θ)).
DIC was derived as a measure of Bayesian model complexity and can be considered as a Bayesian counterpart of AIC (Ding et al. 2018b).
DIC makes weaker assumptions and automatically estimates a penalty for model complexity that is automatically calculated by the WinBUGS program (Spiegelhalter et al. 2003; Crainiceanu et al. 2005; Kéry and Schaub 2011).
Although its properties are uncertain (Spiegelhalter et al. 2002), DIC is rapidly gaining popularity in ecology (Bolker et al. 2009). This may be due to the following three reasons: (1) DIC in concept is readily connected to AIC (Akaike 1974; Ding et al. 2018b); in DIC the MLE and model dimension in AIC are replaced with the posterior mean and effective number of parameters, respectively. (2) DIC has some computational advantages for comparing complex models whose likelihood functions may not even be in analytic forms compared to AIC (Ding et al. 2018b). (3) In Bayesian settings, we can use MCMC tools to simulate posterior distributions of each candidate model, which can be further used to efficiently compute DIC (Ding et al. 2018b). DIC is not yet widely used in microbiome field. We are looking forward to seeing more DIC applications in microbiome study.
16.5.3.7 GICλ (Generalized Information Criterion)
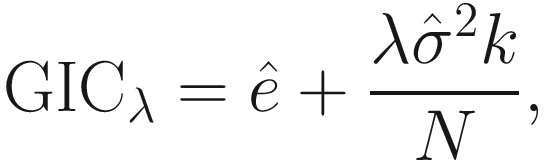
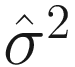is an estimator of σ2 (the variance of the noise), and 
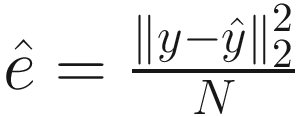is the mean square error between the observations and least-squares estimates under the regression model. λ is a deterministic sequence of N for controlling the trade-off between the model fitting and model complexity. GICλ has the following characteristics:The regression model that minimizes GICλ will be selected.
It was shown (Shao 1997; Ding et al. 2018b) under mild conditions that minimizing GICλ is equivalent to minimizing
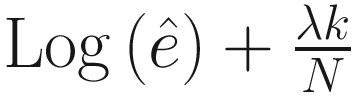if replacing 
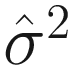with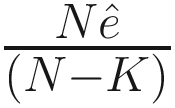 
.In the case, when λ = 2, the formula corresponds to AIC, and λ = log N corresponds to BIC, while Mallows’s Cp method (Mallows 1973) is a special case of GIC with
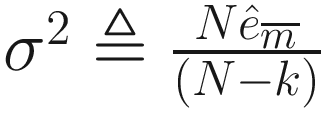and λ = 2, where 
indexes the largest model that includes all of the covariates.
16.5.4 Likelihood-Ratio Test
Likelihood-ratio test (LRT) (Felsenstein 1981; Huelsenbeck and Crandall 1997; Huelsenbeck and Rannala 1997) is a class of tests that compare two competing statistical models based on the ratio of their likelihoods via assessing the goodness of fit. LRT is usually used to compare the nested (null hypothesis) and reference (complex) models defining a hypothesis being tested. LRT statistic is defined as:
![$$ {\lambda}_{\mathrm{LRT}}=-2\ln \left[\frac{L_s\left(\hat{\theta}\right)}{L_g\left(\hat{\theta}\right)}\right], $$](images/486056_1_En_16_Chapter_TeX_Equ12.png)
The log-likelihoods version of LRT, which is expressed as a difference between the log-likelihoods, is mathematically handled and most often used because they can be expressed in terms of deviance:
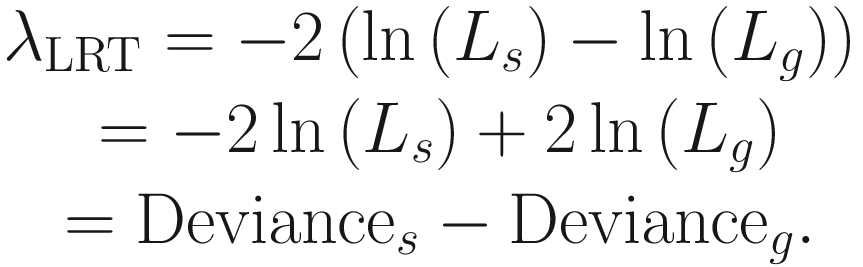
This LRT statistic approximately (asymptotically) follows a χ2 distribution, with degrees of freedom equal to the difference in the number of parameters between the two models.
LRT tests whether likelihood-ratio is significantly different from 1, or equivalently whether its natural logarithm is significantly different from 0.
LRT can be used to test for fixed-effect parameters and covariance parameters.
To test the fixed-effect parameters: (1) Maximum likelihood (ML) estimation is used by setting the same set of covariance parameters but assuming different sets of fixed-effect parameters between the nested and reference models. (2) The difference of log-likelihood for the reference model from that for the nested model. (3) Restricted maximum likelihood (REML) test statistic is obtained by subtracting the −2 ML estimation is not appropriate in testing fixed-effect parameters (Morrell 1998; Pinheiro and Bates 2000; Verbeke and Molenberghs 2000; West et al. 2007).
To test the covariance parameters: (1) REML estimation should be used by setting the same set of fixed-effect parameters but assuming different sets of covariance parameters. (2) The test statistic for covariance parameters is obtained by subtracting the −2 REML log-likelihood value for the reference model from that for the nested model. (3) REML estimation has been shown to reduce the bias inherent in ML estimates of covariance parameters (West et al. 2007; Morrell 1998).
Testing the covariance parameters had to deal with the null hypothesis values lie on the boundary of the parameter space. Because standard deviations (σ) must be larger or equal to 0, the null hypothesis for random effects (σ = 0) violates the assumption that the parameters are not on the boundary (Molenberghs and Verbeke 2007; Bolker et al. 2009).
The way that LRT chooses the better of a pair of nested models via pairwise comparisons has been criticized as abusing the hypothesis testing (Burnham and Anderson 2002; Whittingham et al. 2006; Bolker et al. 2009).
LRT compares the change in deviance between nested and reference models with random-effect terms. This is conservative and hence increasing the risk of type II errors (Bolker et al. 2009).
LRT is associated with stepwise deletion procedures, which have been criticized being prone to overestimate the effect size of significant predictors (Whittingham et al. 2006; Forstmeier and Schielzeth 2011; Burnham et al. 2011); and because stepwise deletion is prone to bias effect sizes, presenting means and SEs of parameters from the reference (complex) model should be more robust, especially when the ratio of data points (observations) (n) to estimated parameters (k) is low (Forstmeier and Schielzeth 2011; Harrison et al. 2018).
It seems that achieving a “minimal adequate model” by using stepwise deletion with LRT only requires a single a priori hypothesis. But in fact it requires multiple significance tests (Whittingham et al. 2006; Forstmeier and Schielzeth 2011); and such cryptic multiple testing can lead to hugely inflated Type I errors (Forstmeier and Schielzeth 2011; Harrison et al. 2018).
In summary, LRT is widely used throughout statistics, but it has some critical weaknesses such as tending to produce “anticonservative” P-values especially in unbalanced data or when the ratio of data points (n) to estimated parameters (k) is low (Pinheiro and Bates 2000) (p. 88) (see Chap. 15 for details), causing biased effect sizes and inflated Type I errors. Thus, LRT is only appropriate for testing fixed effects for both large ratio of the total sample size to the number of fixed effect levels being tested (Pinheiro and Bates 2000) and large number of random effect levels (Agresti 2002; Demidenko 2013); otherwise LRT can be unreliable for fixed effects in GLMMs. Since it is unfortunate that these two conditions are often for most ecological datasets, LRT is not recommended for testing fixed effects with both small total sample size and numbers of random effect levels in ecology (Bolker et al. 2009). LRT has been reviewed (Bolker et al. 2009) in general appropriate for inference on random effects (Scheipl et al. 2008).
16.5.5 Vuong Test
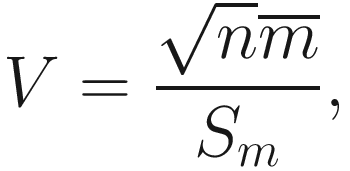
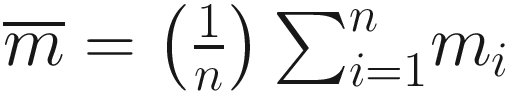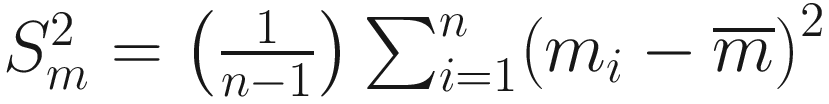and 
, and ![$$ {m}_i=\log \left[\frac{f_1\left({y}_i\right)}{f_2\left({y}_i\right)}\right] $$](images/486056_1_En_16_Chapter_TeX_IEq16.png)
, f1 and f2 are two competing probability models. Vuong test has the following characteristics:Vuong’s statistic is the average log-likelihood ratio suitably normalized and thus has an asymptotically standard normal distribution.
The test is directional, with a large positive (negative) value favoring f1 (f2), and a value close to zero indicating that neither model fits the data well (Vuong 1989; Long 1997; Xia et al. 2012).
In practice, we need to choose a critical value, c, for a significance level. When V > c, the statistic favors the model in the numerator, when V < −c, the statistic favors the model in the denominator, and when V ∈ (−c, c) neither model is favored. It is often to set c as 1.96 for being consistent with standard convention α = 0.05.
16.6 Summary
In this chapter we overviewed the generalized linear mixed models (GLMMs). Section 16.1 briefly reviewed the history of generalized linear models (GLMs) and generalized nonlinear models (GNLMs). Sections 16.2 and 16.3 introduced GLMMs and their model estimations, respectively.
In Sect. 16.4, we comprehensively compared four algorithms for parameter estimation in GLMMs, including (1) penalized quasi-likelihood-based methods using Taylor-series linearization; (2) likelihood-based methods using numerical integration (Laplace approximation, Gauss-Hermite quadrature (GHQ), adaptive Gauss-Hermite quadrature (AGQ)); (3) Markov chain Monte Carlo (MCMC)-based integration; and (4) IWLS (iterative weighted least squares) and EM-IWLS algorithms. Particularly, we introduced the extensions of IWLS algorithm for fitting GLMMs in microbiome data. In Sect. 16.5, we investigated the statistical hypothesis testing and modeling in GLMMs. In this section, we first briefly introduced model selection in statistics and in machine learning; we then described and discussed the three important kinds of criteria/tests for model selection: information criteria, likelihood-ratio test (LRT), and Vuong test. For information criteria, we introduced AIC(Akaike’s information criterion), AICc (finite-sample corrected AIC), QAIC and QAICc (quasi Akaike information criterion and corrected quasi-AIC), BIC (Bayesian information criterion), BC (bridge criterion), DIC (deviance information criterion), and GICλ (generalized information criterion).
Chapter 17 will introduce generalized linear mixed models for longitudinal microbiome data.